Kadane's Algorithm

Understanding Kadane's Algorithm: Solving Subarray Sum Problems

Kadane's Algorithm is a dynamic programming technique that has found its home in competitive programming and technical interviews due to its efficiency in solving problems related to subarrays. This algorithm provides an elegant solution to a variety of challenges involving subarray sums, enabling programmers to tackle such problems with ease and confidence.

The Core Idea

At its heart, Kadane's Algorithm is designed to find the maximum sum of a subarray within a given array. This can be incredibly useful in scenarios where you need to identify the most significant sum attainable from a sequence of elements. Whether you're working with financial data, sensor readings, or any other kind of data stream, this algorithm can quickly pinpoint the highest sum possible within a contiguous subarray.

Example Question: Maximizing Subarray Sums

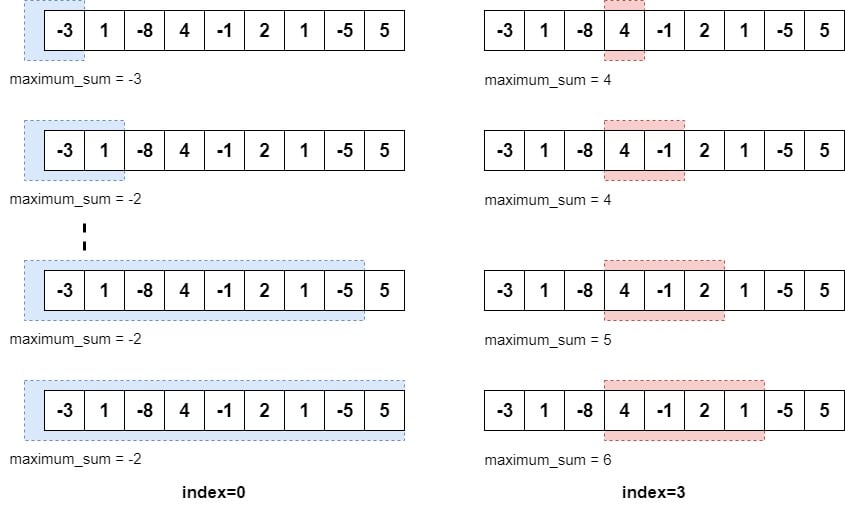
Let's dive into an example question to better understand how Kadane's Algorithm works. Consider the following challenge: Given an array of integers, how can we efficiently calculate the maximum sum of any subarray within the array?

Solution Approach of Kadane's Algorithm

The beauty of Kadane's Algorithm lies in its simplicity. Let's break down the steps involved in solving the aforementioned question using this technique:

1. Initialize two variables, `current` and `max_till_now`, both set to 0. These variables will play a crucial role in keeping track of the current sum and the maximum sum encountered so far.

2. Iterate through the array, element by element, using an index variable `i` ranging from 0 to `n-1`, where `n` represents the length of the array.

3. Update the `current` sum by adding the current element of the array to it: `current += arr[i]`.

4. Update `max_till_now` with the greater value between the current `max_till_now` and the updated `current`: `max_till_now = max(max_till_now, current)`.

5. If the `current` sum becomes negative (i.e., if it's not contributing positively to the sum), reset `current` to 0. This step ensures that we exclude elements that would lead to a negative sum.

6. Repeat steps 3-5 for all elements in the array, traversing from the beginning to the end.

7. Once the loop completes, return the value of `max_till_now` as the final result.

Putting it into Code

Here's how the algorithm looks in Python and C++:

Python Code:

```python

def kadanes_algorithm(arr):

    current = max_till_now = arr[0]

    

    for i in range(1, len(arr)):

        current = max(arr[i], current + arr[i])

        max_till_now = max(max_till_now, current)

        if current < 0:

            current = 0

            

    return max_till_now

# Example usage

arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]

print("Maximum sum of subarray:", kadanes_algorithm(arr))

```

C++ Code:

```cpp

#include <iostream>

#include <algorithm>

using namespace std;

int kadanes_algorithm(int arr[], int n) {

    int current = arr[0];

    int max_till_now = arr[0];

    

    for (int i = 1; i < n; ++i) {

        current = max(arr[i], current + arr[i]);

        max_till_now = max(max_till_now, current);

        if (current < 0) {

            current = 0;

        }

    }

    

    return max_till_now;

}

int main() {

    int arr[] = {-2, 1, -3, 4, -1, 2, 1, -5, 4};

    int n = sizeof(arr) / sizeof(arr[0]);

    cout << "Maximum sum of subarray: " << kadanes_algorithm(arr, n) << endl;

    return 0;

}

```

Summary

 Kadane's Algorithm is a Dynamic programming algorithm that is used in compitetive programming, and technical interviews . Its Useful in solving problems related to subaarays. 

the basic idea:

example question: calculate max sum of subarrays using given array?

solution approach of kadane's algo:

we will initialize two variables 'current' and 'max_till_now' as 0, the 'current' will keep track to the current sum in the array , while 'max_till_now' will keep track of the maximum sum till current.

if current becomes less than 0 , we again initialize current as 0, this is because we want to ignore element of array that contribute to 'negetive sum result'.

we will run the loop until the last element of the array.

after loop ends we return 'max_till_now'.

Conclusion

Kadane's Algorithm is a powerful technique that empowers programmers to solve complex problems involving subarrays and maximum sums with ease. Its efficiency and simplicity make it an essential tool in a programmer's toolkit, especially in competitive programming and technical interviews. By understanding the algorithm's core idea and solution approach, you can confidently tackle a wide range of subarray sum challenges and optimize your problem-solving skills. So, the next time you encounter a problem related to subarrays, consider leveraging Kadane's Algorithm for an elegant and efficient solution.